Introduction
저는 전기전자공학부 학생으로 해당 내용을 정식으로 배운 것은 아닙니다. 양자정보이론을 공부하면서 tensor product 이야기가 많이 나오길래 tensor가 구체적으로 무엇인지 궁금하여 공부하다가 tensor calculus 분야가 재밌어보여서 공부를 시작하였습니다. 혹시라도 포스팅 된 내용에서 부족한 내용이 있다면 댓글 달아주시면 감사드리겠습니다!
Tensor Calculus란 무엇인가?
왜 Tensor에 관심을 갖게 되셨나요? Tensor에 대해 관심을 갖고 공부하시는 이유는 다음과 같을 것입니다.
- 기하학(Geometry)을 더 깊이 있게 공부하기 위해서
- 아인슈타인 상대성이론을 이해하기 위해서
- 양자역학 및 양자컴퓨팅에 대해 더 자세히 이해하기 위해서
저는 상대성이론에 대해 잘 모르지만, 아인슈타인 상대성이론에서는 Einsten's Field Equations(아인슈타인 장 방정식)이 나온다고 합니다. 아래는 그 방정식입니다.
$$R_{\mu\nu}-\frac{1}{2}Rg_{\mu\nu}+\Lambda g_{\mu\nu} = \frac{8\pi G}{c^{4}}T_{\mu\nu}$$
위의 식에서 $g_{\mu\nu}$는 metric tensor라는 것입니다. Metric Tensor가 무엇인지는 뒤에서 설명드리겠습니다.
양자역학 및 양자컴퓨팅에서는 양자 상태들이 벡터로 표현되고, 서로 다른 계의 양자상태들을 표현할 때 Tensor Product 기호를 사용합니다. Tensor가 무엇인지 잘 모르더라도 양자컴퓨팅 내용을 공부하는데 무리는 없지만 이 Tensor라는 것이 무엇인지 이해하고 넘어가면 더 재미있고 속이 편할 것입니다. 아래는 양자컴퓨팅에서 양자상태를 표현할 때 주로 나오는 표현입니다.
$$\vert \psi \rangle \otimes \vert \phi \rangle$$
그렇다면 Tensor는 무엇일까요?
Machine learning을 공부하신 분이라면 tensor를 다차원 배열정도로 생각하실 수 있습니다.
위키피디아에서는 "In mathematics, a tensor is an algebraic object that describes a multilinear relationship between sets of algebraic objects related to a vector space."라고 말합니다. 즉, 좌표계에 상관없이 불변하며, 좌표계의 변화에 따라 표현 방식이 달라질 수 있는 대수적 객체를 말합니다. Tensor를 vector와 covector들이 tensor product에 의해 연결되어 있는 것이라고 말하는 경우도 있습니다.
Tensor의 대표적인 예시인 벡터를 생각해봅시다.

위 그림의 왼쪽과 오른쪽의 검은색 벡터는 서로 같은 벡터입니다. 평행이동을 하면 서로 완전히 겹칩니다.
하지만 노란색과 초록색을 basis로 하는 좌표계를 이용하여 표현할 때와,
파란색과 빨간색을 basis로 하는 좌표계를 이용하여 표현할 때, 검은색 벡터를 표현하기 위한 basis앞에 붙는 계수는 달라집니다.
$$\vert \text{black} \rangle = 3 \vert \text{yellow} \rangle + 4 \vert \text{green} \rangle = 2 \vert \text{blue} \rangle + 3 \vert \text{red} \rangle $$
즉, 좌표계에 상관없이 불변의 값인 벡터는 좌표계의 변화에 따라 basis 앞에 붙은 계수가 달라짐을 확인할 수 있습니다.
Tensor Caluculus를 공부하기 위해 알아야할 배경지식은 무엇인가?
Tensor Calculus를 공부하기 위해 알아야할 배경지식은 다음과 같습니다.
- Multi-Variable Calculus: 학부 1학년 때 주로 배우는 기초 미적분학에서 다루는 내용 정도
- Linear Algebra
- Tensor Algebra
Tensor Algebra에 대해 잘 모르시는 분은 Tensor Calculus관련 포스팅을 보시기 전에 Tensor Algebra 내용 중에서 다음 내용 정도만 공부하시면 좋을 것 같습니다.
- Forward & Backward Transformation
- Vectors
- Covectors
- Metric Tensor
위 4가지에 대해 아래에서 간단히 언급하고 넘어가겠습니다.
Tensor Algebra 배경지식
Forward & Backward Transformation

먼저 벡터의 Forward & Backward Transformation에 대해 생각해봅시다.
Old basis와 New basis가 위의 그림과 같을 때 우리는 저기서 다음과 같은 관계를 찾을 수 있습니다.
먼저 New basis를 Old basis를 이용하여 표현하면 다음과 같습니다.
$$\begin{align} \widetilde{\overrightarrow{e_{1}}} &= 2\overrightarrow{e_{1}}+1\overrightarrow{e_{2}} \\ \widetilde{\overrightarrow{e_{2}}} &= -\frac{1}{2}\overrightarrow{e_{1}}+\frac{1}{4}\overrightarrow{e_{2}} \end{align}\label{eqn1} \tag{1}$$
이번에는 Old basis를 New basis를 이용하여 표현해 보겠습니다.
$$ \begin{align} \overrightarrow{e_{1}} &= \frac{1}{4} \widetilde{\overrightarrow{e_{1}}}-1 \widetilde{\overrightarrow{e_{2}}} \\ \overrightarrow{e_{2}} &= \frac{1}{2}\widetilde{\overrightarrow{e_{1}}}+2\widetilde{ \overrightarrow{e_{2}}} \end{align}\label{eqn2} \tag{2} $$
이 관계를 행렬로 표현하면 다음과 같습니다.
$$\begin{bmatrix} \widetilde{\overrightarrow{e_{1}}} & \widetilde{\overrightarrow{e_{2}}} \\ \end{bmatrix} = \begin{bmatrix} \overrightarrow{e_{1}} & \overrightarrow{e_{2}} \\ \end{bmatrix} \begin{bmatrix} 2 & -\frac{1}{2} \\ 1 & \frac{1}{4} \\ \end{bmatrix}$$
$$\begin{bmatrix} \overrightarrow{e_{1}} & \overrightarrow{e_{2}} \\ \end{bmatrix} = \begin{bmatrix} \widetilde{\overrightarrow{e_{1}}} & \widetilde{\overrightarrow{e_{2}}} \\ \end{bmatrix} \begin{bmatrix} \frac{1}{4} & \frac{1}{2} \\ -1 & 2 \\ \end{bmatrix}$$
이 때, $F= \begin{bmatrix} 2 & -\frac{1}{2} \\ 1 & \frac{1}{4} \\ \end{bmatrix}$, $B = \begin{bmatrix} \frac{1}{4} & \frac{1}{2} \\ -1 & 2 \\ \end{bmatrix}$라고 두면 위의 식을 아래와 같이 표현할 수 있습니다.
$$\label{forward1} \tag{3} \begin{bmatrix} \widetilde{\overrightarrow{e_{1}}} & \widetilde{\overrightarrow{e_{2}}} \\ \end{bmatrix} = \begin{bmatrix} \overrightarrow{e_{1}} & \overrightarrow{e_{2}} \\ \end{bmatrix} F$$
$$ \label{backward1} \tag{4} \begin{bmatrix} \overrightarrow{e_{1}} & \overrightarrow{e_{2}} \\ \end{bmatrix} = \begin{bmatrix} \widetilde{\overrightarrow{e_{1}}} & \widetilde{\overrightarrow{e_{2}}} \\ \end{bmatrix} B$$
수식 $(\ref{forward1})$과 같이 이전의 것에서 새로운 것으로 변환하는 과정을 forward transformation이라고 하며,
수식 $(\ref{backward1})$와 같이 새로운 것에서 다시 이전의 것으로 변환하는 과정을 backward transformation이라고 합니다.
이를 n개의 basis로 일반화하면 다음과 같이 쓸 수 있습니다.
$$F=\begin{bmatrix} F_{11} & F_{12} & \cdots & F_{1n} \\ F_{21} & F_{22} & \cdots & F_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ F_{n1} & F_{n2} & \cdots & F_{nn} \\ \end{bmatrix}$$
$$\begin{align*} \widetilde{\overrightarrow{e_{1}}} &= F_{11}\overrightarrow{e_{1}} + F_{21}\overrightarrow{e_{2}} + \cdots + F_{n1}\overrightarrow{e_{n}} \\ \vdots \\ \widetilde{\overrightarrow{e_{n}}} &= F_{1n}\overrightarrow{e_{1}} + F_{2n}\overrightarrow{e_{2}} + \cdots + F_{nn}\overrightarrow{e_{n}} \end{align*}$$
$$ \therefore \widetilde{\overrightarrow{e_{i}}} = \sum_{j=1}^{n} F_{ji}\overrightarrow{e_{j}}$$
비슷한 과정을 거치면 Backward Transformation 식도 아래와 같이 쓸 수 있습니다.
$$\overrightarrow{e_{i}} = \sum_{j=1}^{n} B_{ji} \widetilde{\overrightarrow{e_{j}}}$$
이 때, 다음의 식을 통해 $F$와 $B$가 서로 inverse matrix라는 것을 알 수 있습니다.
$$\begin{align*} \overrightarrow{e_{i}} &= \sum_{j} B_{ji} \widetilde{\overrightarrow{e_{j}}} \\ &= \sum_{j} B_{ji} \sum_{k} F_{kj} \overrightarrow{e_{k}} \\ &= \sum_{k} \left( \sum_{j} F_{kj}B_{ji} \right) \overrightarrow{e_{k}} \end{align*} $$
$$ \therefore \sum_{j} F_{kj}B_{ji} = \delta_{ik}$$
$$ \Rightarrow FB = I $$
Vector Components transformation

먼저 예시를 보면서 Components Transformation에 대해 알아봅시다.
아시다시피 현재 $F$와 $B$는 다음과 같습니다.
$F= \begin{bmatrix} 2 & -\frac{1}{2} \\ 1 & \frac{1}{4} \\ \end{bmatrix}$, $B = \begin{bmatrix} \frac{1}{4} & \frac{1}{2} \\ -1 & 2 \\ \end{bmatrix}$
위의 그림의 $ \overrightarrow{v} $를 old basis와 new basis를 이용하여 표현해보겠습니다.
$$ \begin{align*} \overrightarrow{v} &= 1 \overrightarrow{e_{1}} + \frac{3}{2} \overrightarrow{e_{2}} = {\begin{bmatrix} 1 \\ 1.5 \\ \end{bmatrix}}_{\overrightarrow{e_{i}}} \\ \overrightarrow{v} &= 1 \widetilde{\overrightarrow{e_{1}}} + 2 \widetilde{\overrightarrow{e_{2}}} = {\begin{bmatrix} 1 \\ 2 \\ \end{bmatrix}}_{\widetilde{\overrightarrow{e_{i}}}}\end{align*} $$
그리고 이 두 표현법은 다음의 관계를 가지는 것을 알 수 있습니다.
$$ \begin{align*} {\begin{bmatrix} 1 \\ 2 \\ \end{bmatrix}}_{\widetilde{\overrightarrow{e_{i}}}} &= B {\begin{bmatrix} 1 \\ 1.5 \\ \end{bmatrix}}_{\overrightarrow{e_{i}}} \\ {\begin{bmatrix} 1 \\ 1.5 \\ \end{bmatrix}}_{\overrightarrow{e_{i}}} &= F {\begin{bmatrix} 1 \\ 2 \\ \end{bmatrix}}_{\widetilde{\overrightarrow{e_{i}}}} \end{align*} $$
이를 보면 위에서 basis vector의 transformation가 변환 방법이 반대가 되었다는 것을 알 수 있습니다.
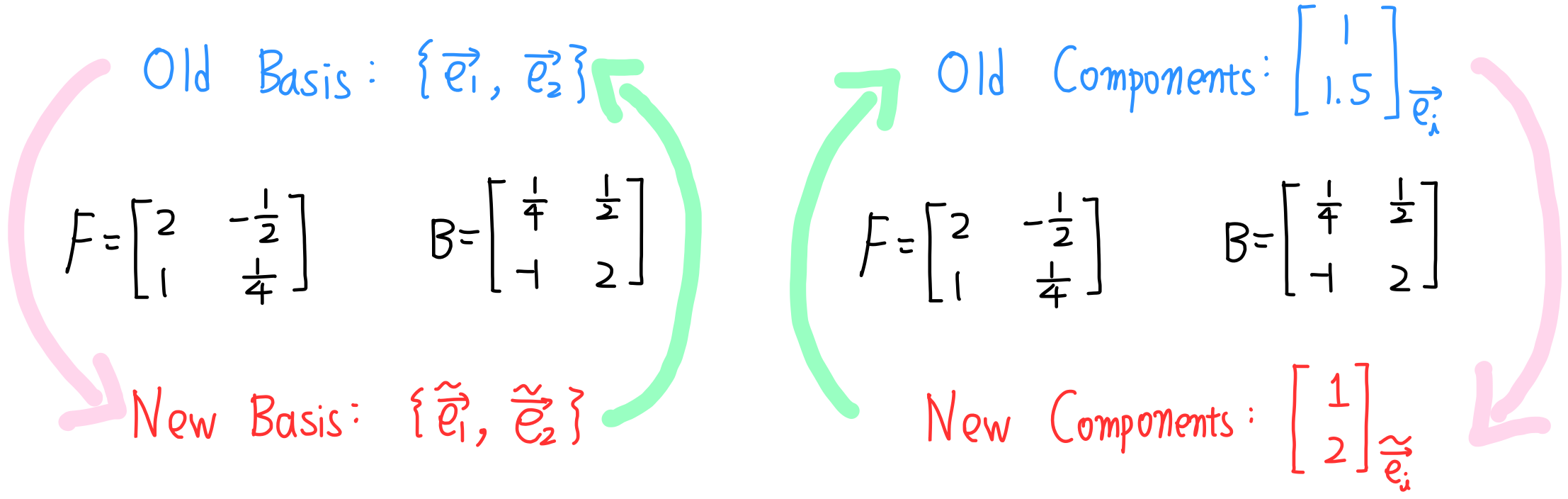
이러한 Vector Components Transformation을 수식적으로 보이겠습니다.
$$ \begin{align*} \overrightarrow{v} = \sum_{j=1}^{n} v_{j} \overrightarrow{e_{j}} = \sum_{i=1}^{n} \widetilde{v_{i}} \widetilde{\overrightarrow{e_{i}}} \end{align*} $$
이 때,
$$ \begin{align*} \overrightarrow{v} &= \sum_{j=1}^{n} v_{j} \overrightarrow{e_{j}} \\ &= \sum_{j=1}^{n} v_{j} \left( \sum_{i=1}^{n} B_{ij} \widetilde{\overrightarrow{e_{i}}}\right) \\ &= \sum_{i=1}^{n} \left( \sum_{j=1}^{n} B_{ij} v_{j} \right) \widetilde{\overrightarrow{e_{i}}} \end{align*} $$
$$ \therefore \widetilde{v_{i}} = \sum_{j=1}^{n} B_{ij} v_{j} $$
같은 과정을 통해 아래의 식도 유도할 수 있습니다.
$$v_{i} = \sum_{j=1}^{n} F_{ij} \widetilde{v_{j}}$$
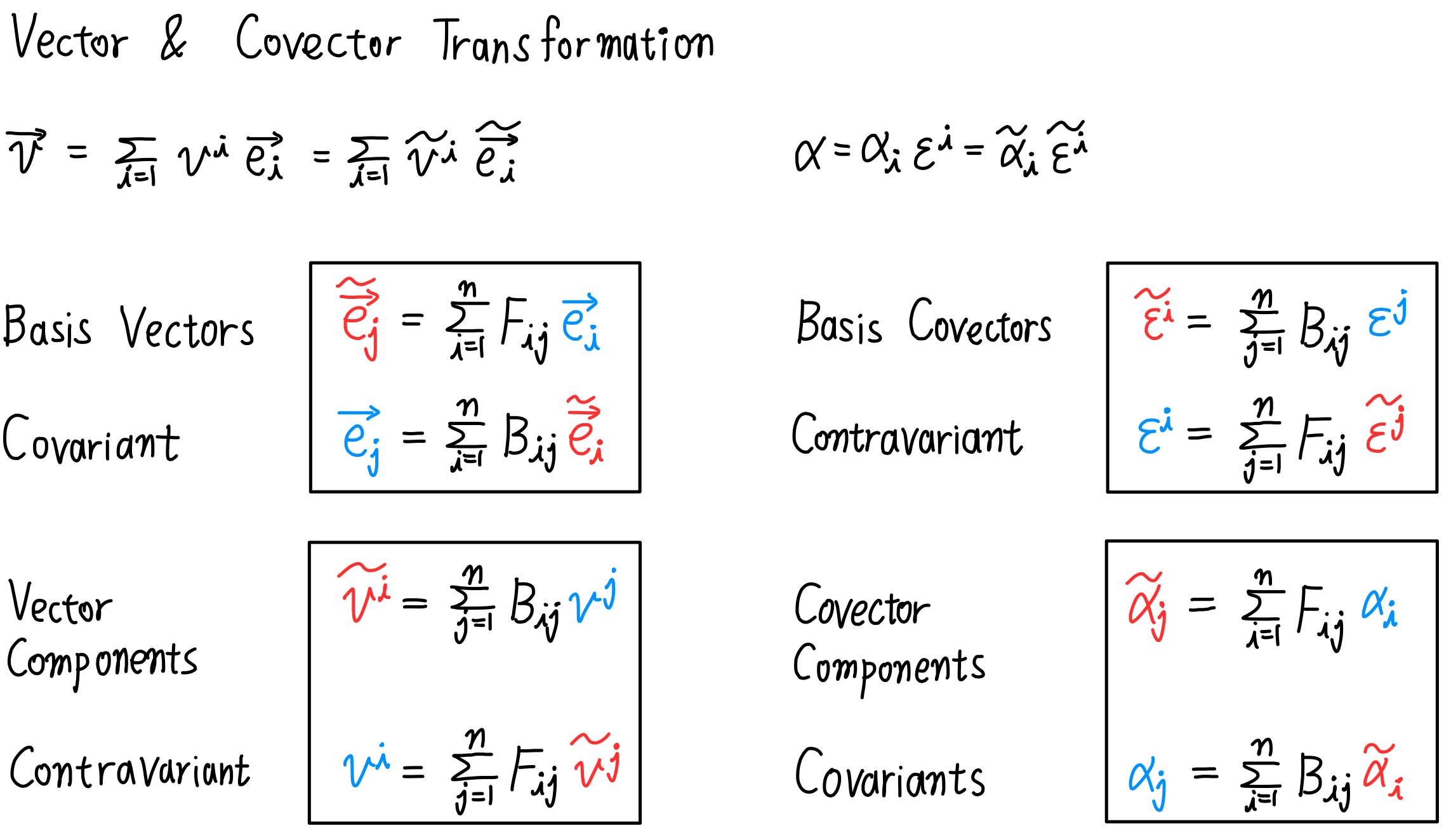
벡터와 관련하여 지금까지 나온 내용들을 정리하면 다음과 같습니다.
$$\widetilde{\overrightarrow{e_{i}}} = \sum_{j=1}^{n} F_{ji}\overrightarrow{e_{j}}$$
$$\overrightarrow{e_{i}} = \sum_{j=1}^{n} B_{ji} \widetilde{\overrightarrow{e_{j}}}$$
$$\widetilde{v_{i}} = \sum_{j=1}^{n} B_{ij} v_{j}$$
$$v_{i} = \sum_{j=1}^{n} F_{ij} \widetilde{v_{j}}$$
Covector
Covector란 vector를 입력으로 받아 scalar값을 출력하는 선형 함수입니다. 행렬로 나타낼 때는 주로 행벡터로 나타냅니다.
Covector의 특성을 정리하자면 다음과 같습니다.
- vector를 입력으로 받아 scalar값을 출력하는 함수입니다. $\alpha : V \to \mathbb{R}$
- $\alpha(\overrightarrow v+\overrightarrow w) = \alpha(\overrightarrow v) + \alpha(\overrightarrow w)$
- $\alpha(n\overrightarrow v) = n\alpha(\overrightarrow v)$
- $(\beta + \gamma)(\overrightarrow v) = \beta(\overrightarrow v) + \gamma(\overrightarrow v)$
- $(n \cdot \alpha)\overrightarrow v = n\alpha(\overrightarrow v)$
Covector 예시를 들어보겠습니다. $\begin{bmatrix} 2 & 1 \end{bmatrix}$ 라는 covector가 있다고 합시다.
이 covector 함수에 $\begin{bmatrix} x \\ y \end{bmatrix}$ 라는 vector가 입력으로 들어가면 출력으로 $\begin{bmatrix} 2 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}=2x+y$ 이라는 scalar 값이 나옵니다.
위 결과를 이용하여 Covector를 등고선처럼 시각화할 수 있습니다.
어떠한 상수 $k$에 대해 $2x+y=k$를 만족하는 점 $(x, y)$의 집합을 그리는 것입니다.
Covector $\begin{bmatrix} 2 & 1 \end{bmatrix}$ 를 시각화 한 결과는 다음과 같습니다.
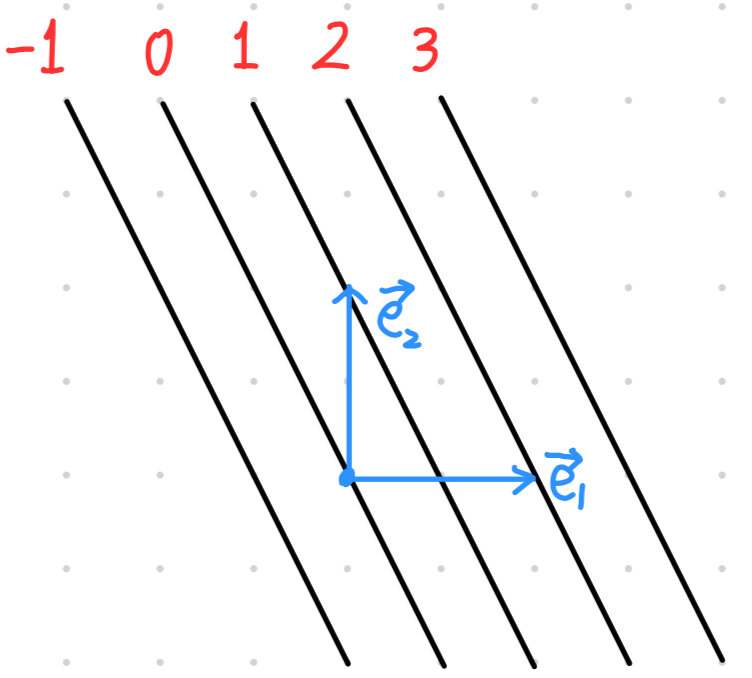
위와 같이 그린 것을 convector field라고 합니다. 이러한 covector field 시각화는 매우 유용합니다.
어떠한 covector에 임의의 vector $\overrightarrow{v}$ 가 입력으로 들어왔을 때, 결과값은 그 벡터가 covector field의 선을 몇개를 관통했는지를 보면 되기 때문입니다.

임의의 vector $\overrightarrow v$ 는 $\{\overrightarrow{e_i}\}$ 라는 basis vector set이 주어지면 $\overrightarrow v = \sum_i v^i \overrightarrow{e_i}$ 와 같이 쓸 수 있습니다.
그렇다면 Covector의 basis는 어떤 방식으로 쓸 수 있을까요?
다음의 두 가지 특별한 covector를 봅시다. $\epsilon^1,\, \epsilon^2: V \to \mathbb{R}$ 이라고 할 때,
$$\epsilon^1(\overrightarrow{e_1}) = 1,\qquad \epsilon^1(\overrightarrow{e_2}) = 0$$
$$\epsilon^2(\overrightarrow{e_1}) = 0,\qquad \epsilon^2(\overrightarrow{e_2}) = 1$$
하나의 수식으로 정리하자면 다음과 같습니다.
$$\epsilon^i(\overrightarrow{e_j}) = \delta_{ij}$$
임의의 vector $\overrightarrow{v} = v^1 \overrightarrow{e_1} + v^2 \overrightarrow{e_2}$가 있다고 합시다.
위에서 정의한 $\epsilon^1$, $\epsilon^2$ 에 $\overrightarrow{v}$ 를 입력으로 넣었을 때 어떠한 결과가 나오는지 보겠습니다.
$$\epsilon^1(\overrightarrow{v}) = \epsilon^1(v^1 \overrightarrow{e_1} + v^2 \overrightarrow{e_2}) = v^1 \epsilon^1(\overrightarrow{e_1}) + v^1 \epsilon^1(\overrightarrow{e_2})=v^1$$
$$\epsilon^2(\overrightarrow{v}) = \epsilon^2(v^1 \overrightarrow{e_1} + v^2 \overrightarrow{e_2}) = v^1 \epsilon^2(\overrightarrow{e_1}) + v^1 \epsilon^2(\overrightarrow{e_2})=v^2$$
정리하자면, 다음과 같은 관계가 성립합니다.
$$\epsilon^i(\overrightarrow{v}) = v^i$$
이번에는 임의의 covector $\alpha$ 에 입력으로 $\overrightarrow{v} = v^1 \overrightarrow{e_1} + v^2 \overrightarrow{e_2}$ 를 넣었을 때 출력되는 값을 보겠습니다.
$$\begin{align*} \alpha(\overrightarrow{v}) &= \alpha \left( v^1 \overrightarrow{e_1} + v^2 \overrightarrow{e_2} \right) \\ &= v^1 \alpha(\overrightarrow{e_1}) + v^2 \alpha(\overrightarrow{e_2}) \\ &= \epsilon^1 (\overrightarrow{v})\alpha(\overrightarrow{e_1}) + \epsilon^2(\overrightarrow{v})\alpha(\overrightarrow{e_2})\end{align*}$$
이 때, $\alpha(\overrightarrow{e_1}) = \alpha_1$, $\alpha(\overrightarrow{e_2}) = \alpha_2$ 이라고 정의합시다. 이들을 covector components라고 부릅니다.
그러면 $ \alpha(\overrightarrow{v})$ 다음과 같이 됩니다.
$$\alpha(\overrightarrow{v}) = \alpha_1\epsilon^1 (\overrightarrow{v}) + \alpha_2\epsilon^2(\overrightarrow{v})$$
여기서 공통으로 있는 $(\overrightarrow{v})$ 를 제거하고 연산자만 남기면 다음과 같은 식을 얻을 수 있습니다.
$$\therefore \alpha = \alpha_1\epsilon^1 + \alpha_2\epsilon^2$$
따라서, $\epsilon^1$ 과 $\epsilon^2$ 는 covector의 basis라고 할 수 있습니다.
Covector Components Transformation
서로 다른 basis의 covector 사이의 transformation에 대해 알아보겠습니다.
이전에 예시로 들었던 covector $\begin{bmatrix} 2 & 1 \end{bmatrix}_{\epsilon^i}$ 에 대해 basis 변화에 따른 covector components를 먼저 비교해보겠습니다.
이전에 다루었던 아래의 그림과 같은 $\overrightarrow{e_1}$, $\overrightarrow{e_2}$ 와 $\widetilde{\overrightarrow{e_1}}$, $\widetilde{\overrightarrow{e_2}}$ 를 다시 갖고 오겠습니다.

다음의 두 covector basis set은 다음과 같이 정의할 수 있습니다.
$$\epsilon^i (\overrightarrow{e_j}) = \delta_{ij}$$
$$\widetilde{\epsilon^i} (\widetilde{\overrightarrow{e_j}}) = \delta_{ij}$$
그리고 우리는 다음과 같은 사실을 압니다.
$$\alpha = \alpha_1 \epsilon^1 + \alpha_2 \epsilon^2 = \widetilde{\alpha_1} \widetilde{\epsilon^1} + \widetilde{\alpha_2} \widetilde{\epsilon^2}$$
$$\alpha_1 = \alpha(\overrightarrow{e_1}) \qquad \alpha_2 = \alpha(\overrightarrow{e_2})$$
$$\widetilde{\alpha_1} = \alpha(\widetilde{\overrightarrow{e_1}}) \qquad \widetilde{\alpha_2} = \alpha(\widetilde{\overrightarrow{e_2}})$$
현재 우리는 covector $\begin{bmatrix} 2 & 1 \end{bmatrix}_{\epsilon^i}$ 를 다루고 있습니다.
따라서 $\alpha_1=2$, $\alpha_2=1$ 입니다.
수식 $(\ref{eqn1})$ 을 이용하여 다음과 같이 $\widetilde{\alpha_1}$ 와 $\widetilde{\alpha_2}$ 를 구할 수 있습니다.
$$\begin{align} \widetilde{\alpha_1} &= \alpha(\widetilde{\overrightarrow{e_1}}) \\ &= \alpha(2\overrightarrow{e_1} + 1\overrightarrow{e_2}) \\ &= 2\alpha(\overrightarrow{e_1}) + 1\alpha(\overrightarrow{e_2}) \\ &= 2 \alpha_1 + 1\alpha_2 \\ &=2\times2 + 1\times1 \\ &= 5 \end{align}$$
비슷한 방식으로,
$$\widetilde{\alpha_2} = -\dfrac{3}{4}$$
따라서 $\begin{bmatrix} 2 & 1 \end{bmatrix}_{\epsilon^i}$ 를 new basis로 vector components transformation을 한 결과는 $\begin{bmatrix} 5 & -\dfrac{3}{4} \end{bmatrix}_{\widetilde{\epsilon^i}}$ 입니다.
앞에서, $F= \begin{bmatrix} 2 & -\frac{1}{2} \\ 1 & \frac{1}{4} \\ \end{bmatrix}$, $B = \begin{bmatrix} \frac{1}{4} & \frac{1}{2} \\ -1 & 2 \\ \end{bmatrix}$ 이라고 하였습니다.
그럼 covector components transformation은 다음과 같이 된다는 것을 확인 할 수 있습니다.
$$\begin{bmatrix} 5 & -\dfrac{3}{4} \end{bmatrix}_{\widetilde{\epsilon^i}}=\begin{bmatrix} 2 & 1 \end{bmatrix}_{\epsilon^i}F$$
$$\begin{bmatrix} 2 & 1 \end{bmatrix}_{\epsilon^i}=\begin{bmatrix} 5 & -\dfrac{3}{4} \end{bmatrix}_{\widetilde{\epsilon^i}}B$$
즉, covector components transformation은 basis vector trasnformation과 같은 covariant transformation이라는 것을 알 수 있습니다. $\widetilde{\alpha_1}$, $\widetilde{\alpha_2}$ 를 구하는 과정을 보시면 변환 과정이 basis vector transformation과 같을 수 밖에 없다는 것을 알 수 있습니다.
Covector Transformation Rules
위에서는 covector components transformation 하는 방법을 예시를 통해 살펴보았습니다.
이번에는 covector의 basis라 할 수 있는 $\epsilon^1$, $\epsilon^2$ 와 $\widetilde{\epsilon^1}$, $\widetilde{\epsilon^2}$ 사이의 관계에 대해 살펴보겠습니다.
우선 수식 $(\ref{eqn1})$ 을 갖고 오겠습니다.
$$\begin{align} \widetilde{\overrightarrow{e_{1}}} &= 2\overrightarrow{e_{1}}+1\overrightarrow{e_{2}} \\ \widetilde{\overrightarrow{e_{2}}} &= -\frac{1}{2}\overrightarrow{e_{1}}+\frac{1}{4}\overrightarrow{e_{2}} \end{align}$$
위의 식처럼 $\epsilon^1$, $\epsilon^2$ 와 $\widetilde{\epsilon^1}$, $\widetilde{\epsilon^2}$ 도 다음과 같은 관계가 있을 것입니다.
$$\begin{align*} \widetilde{\epsilon^1} &= Q_{11} \epsilon^1 + Q_{12}\epsilon^2 \\ \widetilde{\epsilon^2} &= Q_{21} \epsilon^1 + Q_{22}\epsilon^2 \end{align*}$$
그럼 다음과 같은 수식들이 성립합니다.
$$\begin{align*} \widetilde{\epsilon^1}\left(\widetilde{\overrightarrow{e_1}}\right) &= Q_{11} \epsilon^1\left(\widetilde{\overrightarrow{e_1}}\right) + Q_{12}\epsilon^2\left(\widetilde{\overrightarrow{e_1}}\right) = Q_{11} \\ \widetilde{\epsilon^1}\left(\widetilde{\overrightarrow{e_2}}\right) &= Q_{12} \\ \widetilde{\epsilon^2}\left(\widetilde{\overrightarrow{e_1}}\right) &= Q_{21} \\ \widetilde{\epsilon^2}\left(\widetilde{\overrightarrow{e_2}}\right) &= Q_{22}\end{align*}$$
따라서 $\epsilon^1$, $\epsilon^2$ 와 $\widetilde{\epsilon^1}$, $\widetilde{\epsilon^2}$ 의 관계를 다음과 같이 표현할 수 있습니다.
$$\begin{align*} \widetilde{\epsilon^1} &= \widetilde{\epsilon^1}\left(\widetilde{\overrightarrow{e_1}}\right) \epsilon^1 + \widetilde{\epsilon^1}\left(\widetilde{\overrightarrow{e_2}}\right)\epsilon^2 \\ \widetilde{\epsilon^2} &= \widetilde{\epsilon^2}\left(\widetilde{\overrightarrow{e_1}}\right) \epsilon^1 + \widetilde{\epsilon^2}\left(\widetilde{\overrightarrow{e_2}}\right)\epsilon^2 \end{align*}$$
수식 $(\ref{eqn2})$ 에 따라 이것을 구체적으로 구해보면 다음과 같이 됩니다.
$$\begin{align*} \widetilde{\epsilon^1} &= \dfrac{1}{4} \epsilon^1 + \dfrac{1}{2}\epsilon^2 \\ \widetilde{\epsilon^2} &= (-1) \epsilon^1 + 2\epsilon^2 \end{align*}$$
이를 통해, covector transformation은 다음과 같이 contravariant 하다는 것을 확인할 수 있습니다.
$$\begin{bmatrix} \widetilde{\epsilon^1} \\ \widetilde{\epsilon^2} \end{bmatrix} = B \begin{bmatrix} \epsilon^1 \\ \epsilon^2 \end{bmatrix}$$
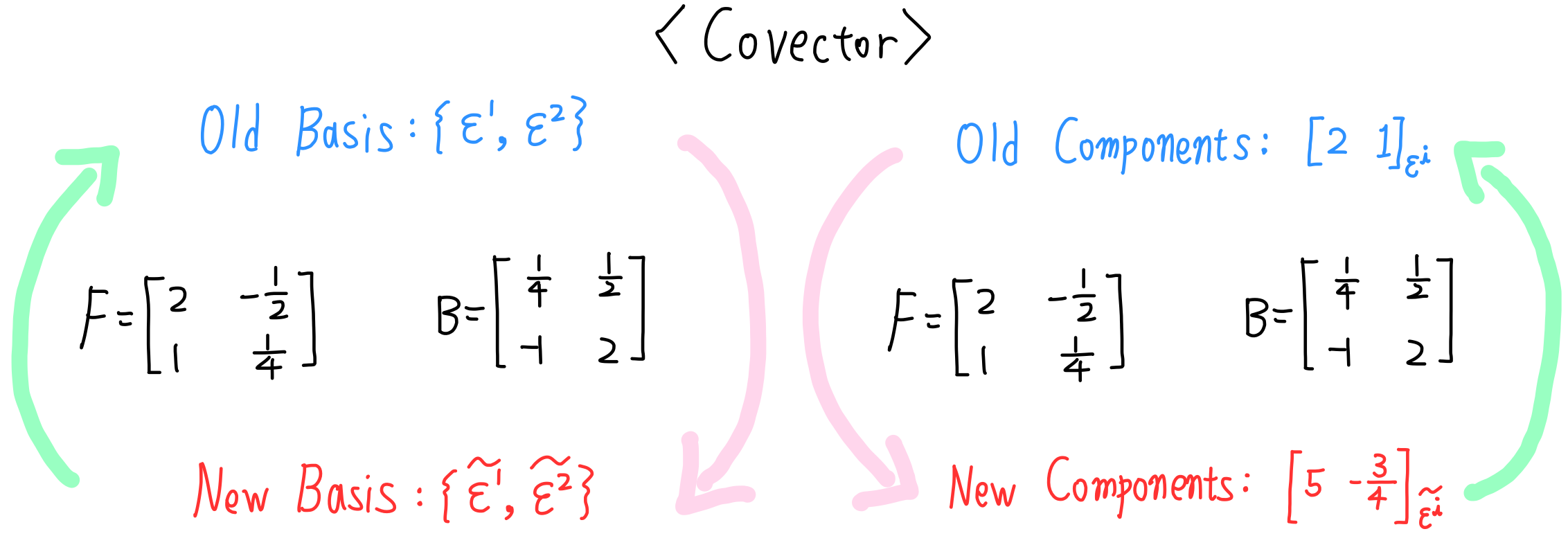
이제는 예시를 통해 알아보는 것이 아니라, 수학적으로 covector transformation rule 수식을 보이겠습니다.
$\widetilde{\epsilon^i}$ 을 다음과 같이 $\epsilon^j$ 에 대한 항으로 표현할 수 있습니다.
$$\widetilde{\epsilon^i} = Q_{i1}\epsilon^1 + Q_{i2}\epsilon^2 + \cdots + Q_{in}\epsilon^n = \sum_{j=1}^n Q_{ij}\epsilon^j$$
$\widetilde{\epsilon^i}\left( \widetilde{\overrightarrow{e_k}}\right) = \delta_{ik}$ 라는 사실을 이용하여 수식을 전개하겠습니다.
$$\begin{align} \widetilde{\epsilon^i}\left( \widetilde{\overrightarrow{e_k}} \right) &= \sum_{j=1}^n Q_{ij}\epsilon^j \left( \widetilde{\overrightarrow{e_k}} \right) \\ \delta_{ik} &= \sum_{j=1}^n Q_{ij}\epsilon^j \left(\sum_{l=1}^n F_{lk} \overrightarrow{e_l}\right) \\ &= \sum_{j=1}^n \sum_{l=1}^n Q_{ij}F_{lk} \epsilon^j \left(\overrightarrow{e_l}\right) \\ &= \sum_{j=1}^n \sum_{l=1}^n Q_{ij}F_{lk} \delta_{jl} \\ &= \sum_{j=1}^n Q_{ij}F_{jk}\end{align}$$
이것을 정리하면 다음과 같습니다.
$$\therefore \delta_{ik} = \sum_{j=1}^n Q_{ij}F_{jk}$$
위의 수식은 $Q=F^{-1}$ 라는 의미이며, 앞에서 $F$ 와 $B$ 가 서로 Inverse matrix임을 보였으므로,
$$Q=B$$
임을 알 수 있습니다.
따라서, 최종적으로 다음과 같은 수식이 성립함을 알 수 있습니다.
$$\widetilde{\epsilon^i} = \sum_{i=1}^n B_{ij}\epsilon^j$$
비슷한 방식으로 다음을 보일 수 있습니다.
$$\epsilon^i = \sum_{i=1}^n F_{ij}\widetilde{\epsilon^j}$$
예시를 통해서 봤던 것과 마찬가지로 contravariant transformation임을 확인할 수 있습니다.
Tensor Algebra 배경지식 총 정리
지금까지 나온 수식을 총 정리 하면 다음 그림과 같이 됩니다.
Metric Tensor
Mectric Tensor는 간단히 언급만 하고 넘어가겠습니다!
Metric Tensor $g$ 는 다음과 같은 것을 의미합니다.
$$g_{\overrightarrow{e_i}} = \begin{bmatrix} \overrightarrow{e_1}\cdot\overrightarrow{e_1} & \overrightarrow{e_1}\cdot\overrightarrow{e_2} \\ \overrightarrow{e_2}\cdot\overrightarrow{e_1} & \overrightarrow{e_2}\cdot\overrightarrow{e_2} \end{bmatrix}$$
$$g_{ij} = \left(\overrightarrow{e_i}\cdot\overrightarrow{e_j}\right)$$
이번 포스트는 여기까지 입니다!
'취미 > 수학' 카테고리의 다른 글
| [tensor calculus] 2. Derivatives are Vectors & Extrinsic vs Intrinsic (0) | 2024.03.06 |
|---|---|
| [tensor calculus] 1. The Jacobian & Einstein summation convention (0) | 2024.03.06 |

