- 왜 미분을 벡터로 볼 수 있을까?
- Vector components 계산 예시
- Derivative Transformation Rules
- Jacobian & Vector components transformation
- Extrinsic vs Intrinsic + New notation
Derivatives are Vectors
이 내용을 잘 이해하기 위해서는 이전 포스트 내용을 알아야 합니다.
https://psg-quantuminfo.tistory.com/35
[tensor calculus] 0. Intorduction
Introduction Tensor Calculus란 무엇인가? Tensor Calculus를 공부하기 위해 알아야할 배경지식은 무엇인가? Tensor Algebra 배경지식 Introduction 저는 전기전자공학부 학생으로 해당 내용을 정식으로 배운 것은
psg-quantuminfo.tistory.com
https://psg-quantuminfo.tistory.com/38
[tensor calculus] 1. The Jacobian & Einstein summation convention
The Jacobian Forward Transformation Backward Transformation Inverse Einstein summation convention 이번 내용을 이해하기 위해서는 벡터의 Forward Transformation, Backward Transformation에 대한 지식이 있으셔야 합니다. 이에 대한
psg-quantuminfo.tistory.com
지지난 포스트인 0. Introduction의 <Tensor Algebra 배경지식> 부분에서 Basis Transformation과 Vector Components Transformation은 서로 반대 과정임을 보였습니다.
이번 포스트에서는 미분을 한 결과가 vector와 똑같이 다룰 수 있다는 것을 설명합니다.
왜 미분을 벡터로 볼 수 있을까?
미분을 먼저 살펴보겠습니다. 여기서는 다변수 미분을 다룹니다.
Input parameter $\lambda$ 에 대해 output으로 vector $\overrightarrow{R}$ 이 나타난다고 합시다.
아래의 그림에서 이를 볼 수 있습니다.

$\overrightarrow{R}$ 의 $\lambda$ 에 대한 미분은 아래와 같이 표현할 수 있습니다.
$$\dfrac{d\overrightarrow{R}}{d\lambda} = \lim_{h \to 0} \dfrac{\overrightarrow{R}(\lambda + h) - \overrightarrow{R}(\lambda)}{h}$$
이를 Cartesian coordinate에서 chain rule을 적용하여 표현하면 다음과 같습니다.
$$\begin{align*} \dfrac{d\overrightarrow{R}}{d\lambda} &= \dfrac{\partial \overrightarrow{R}}{\partial x} \dfrac{d x}{d \lambda} + \dfrac{\partial \overrightarrow{R}}{\partial y} \dfrac{dy}{d \lambda} \\ &= \dfrac{d x}{d \lambda} \dfrac{\partial \overrightarrow{R}}{\partial x} + \dfrac{dy}{d \lambda} \dfrac{\partial \overrightarrow{R}}{\partial y} \\ &= \dfrac{dc^i}{d\lambda} \dfrac{\partial \overrightarrow{R}}{dc^i} \end{align*}$$
위의 수식에서 세번째 줄은 Einstein summation convention을 이용하여 표현한 것입니다.
이제 아래의 수식을 통해 벡터와 미분 식의 구조를 비교해보시길 바랍니다.
$$\begin{align*} \overrightarrow{v} &= v^1 \overrightarrow{e_1} + v^2 \overrightarrow{e_2} = v^i \overrightarrow{e_i}\\ \dfrac{d\overrightarrow{R}}{d\lambda} &= \dfrac{dx}{d\lambda} \dfrac{\partial \overrightarrow{R}}{\partial x} + \dfrac{dy}{d\lambda} \dfrac{\partial \overrightarrow{R}}{\partial y} = \dfrac{dc^i}{d\lambda} \dfrac{\partial \overrightarrow{R}}{\partial c^i} \end{align*}$$
이전 포스트 초반에 tensor calculus에서 partial derivative는 해당 방향의 vector와 같다고 하였습니다.
즉, 위의 수식에서 $ \dfrac{\partial \overrightarrow{R}}{\partial c^i} = \overrightarrow{e_i} $ 입니다.
또한, $v^i$ 는 vector component입니다.
따라서, $\dfrac{dc^i}{d \lambda}$ 는 vector component로 여길 수 있습니다.
이렇게 생각하면 왜 "Derivatives are Vectors"라고 말하는지 알 수 있습니다.
Vector components 계산 예시
$\overrightarrow{R}(\lambda) = (x(\lambda),\, y(\lambda)) = (2 \cos \lambda,\, 2 \sin \lambda)$ 벡터를 $\lambda$ 에 대해 미분하였을 때, Cartesian coordinate에서의 vector components Polar coordinate에서의 vector components를 계산하겠습니다.

Cartesian coordinate
$\overrightarrow{R}(\lambda) = (x(\lambda),\, y(\lambda)) = (2 \cos \lambda,\, 2 \sin \lambda)$ 을 $\lambda$ 에 대해 미분하면 다음과 같습니다.
$$\dfrac{d\overrightarrow{R}}{d\lambda} = \dfrac{dx}{d\lambda} \dfrac{\partial \overrightarrow{R}}{\partial x} + \dfrac{dy}{d\lambda} \dfrac{\partial \overrightarrow{R}}{\partial y}$$
이 때,
$$\begin{align*} \dfrac{dx}{d\lambda} &= \dfrac{d}{d\lambda} 2 \cos \lambda = -2 \sin \lambda \\ \dfrac{dy}{d\lambda} &= \dfrac{d}{d\lambda} 2 \sin \lambda = \; 2 \cos \lambda\end{align*}$$
입니다.
위의 식에 따라서 $\dfrac{d\overrightarrow{R}}{d\lambda}$ 를 다시 표현하면 다음과 같습니다.
$$\begin{align*} \dfrac{d\overrightarrow{R}}{d\lambda} &= -2 \sin \lambda \dfrac{\partial \overrightarrow{R}}{\partial x} + 2 \cos \lambda \dfrac{\partial \overrightarrow{R}}{\partial y} \\ &= \begin{bmatrix} -2 \sin \lambda \\ 2 \cos \lambda \end{bmatrix}_{\frac{\partial \overrightarrow{R}}{\partial c^i}} \end{align*}$$
Polar coordinate
먼저, $r=\sqrt{x^2 + y^2},\; \theta = \tan ^{-1} \left( \dfrac{y}{x} \right)$ 관계를 이용해서 $r(\lambda)$ 와 $\theta(\lambda)$ 를 구해야합니다.
먼저 $r(\lambda)$ 을 구하겠습니다.
$$\begin{align*} r(\lambda) &= \sqrt{(x(\lambda))^2 + (y(\lambda))^2} \\ &= \sqrt{4 \cos^2 \lambda + 4 \sin^2 \lambda}\\ &= \sqrt{4} \\ &= 2\end{align*}$$
다음은 $\theta(\lambda)$ 을 구하겠습니다.
$$\begin{align*} \theta(\lambda) &= \tan^{-1} \left( \dfrac{y(\lambda)}{x(\lambda)}\right) \\ &= \tan^{-1} \left( \dfrac{2 \sin \lambda}{2 \cos \lambda}\right) \\ &= \tan^{-1} \left( \tan \lambda\right) \\ &= \lambda\end{align*}$$
따라서 벡터 $\overrightarrow{R}(\lambda)$는 다음과 같이 표현할 수 있습니다.
$$\overrightarrow{R}(\lambda) = (r(\lambda),\, \theta(\lambda)) = (2,\, \lambda)$$
이제 벡터의 미분 $\dfrac{d \overrightarrow{R}}{d \lambda}$ 을 Chain Rule을 이용하여 전개하겠습니다.
$$\begin{align*} \dfrac{d \overrightarrow{R}}{d \lambda} &= \dfrac{dr}{d\lambda} \dfrac{\partial \overrightarrow{R}}{\partial r} + \dfrac{d \theta}{d \lambda} \dfrac{\partial \overrightarrow{R}}{d \theta} \\ &= \dfrac{d}{d\lambda}(2) \cdot \dfrac{\partial \overrightarrow{R}}{\partial r} + \dfrac{d}{d \lambda} (\lambda) \cdot\dfrac{\partial \overrightarrow{R}}{d \theta} \\ &= 0 \cdot \dfrac{\partial \overrightarrow{R}}{\partial r} + 1 \cdot \dfrac{\partial \overrightarrow{R}}{d \theta} \\ &= \begin{bmatrix} 0 \\ 1 \end{bmatrix}_{\frac{\partial \overrightarrow{R}}{\partial p^i}}\end{align*}$$
정리
$\dfrac{d \overrightarrow{R}}{d \lambda}$ 를 서로 다른 basis에 대해 표현하면 vector components가 달라진다는 것을 보였습니다.
Cartesian coordinate에서는 vector components가 $\begin{bmatrix} -2 \sin \lambda \\ 2 \cos \lambda \end{bmatrix}_{\frac{\partial \overrightarrow{R}}{\partial c^i}}$이고, Polar coordinate에서는 vector components가 $\begin{bmatrix} 0 \\ 1 \end{bmatrix}_{\frac{\partial \overrightarrow{R}}{\partial p^i}}$ 입니다.
Derivative Transformation Rules
예전 포스트인 "[tensor calculus] 0. Introduction" 을 보시면 기본적인 vector compoenets 의 변환은 contravariant(변환을 할 때 반대의 연산자를 가해야 하는 경우. 즉, Forward transformation일 때 Backward transformation matrix를 곱해야 하고, Backward transformation일 때 Forward transformation matrix를 곱하는 형태)임을 보였었습니다.
미분을 벡터로 여겼을 때 나타나는 vector components 사이의 변환 규칙도 contravariant 함을 보이겠습니다.
먼저 다음의 두 표현을 보면서 서로 유사한 형태라는 것을 파악하시길 바랍니다.
$$\overrightarrow{v} = v^i \overrightarrow{e_i} = \widetilde{v}^i \widetilde{\overrightarrow{e_i}}$$
$$\dfrac{d \overrightarrow{R}}{d \lambda} = \dfrac{dc^i}{d\lambda}\dfrac{\partial \overrightarrow{R}}{\partial c^i} = \dfrac{dp^i}{d\lambda}\dfrac{\partial \overrightarrow{R}}{\partial p^i}$$
Review vector component transformation
"[tensor calculus] 0. Introduction"에서 다루었던 vector component transformation 내용을 가볍게 언급하겠습니다.
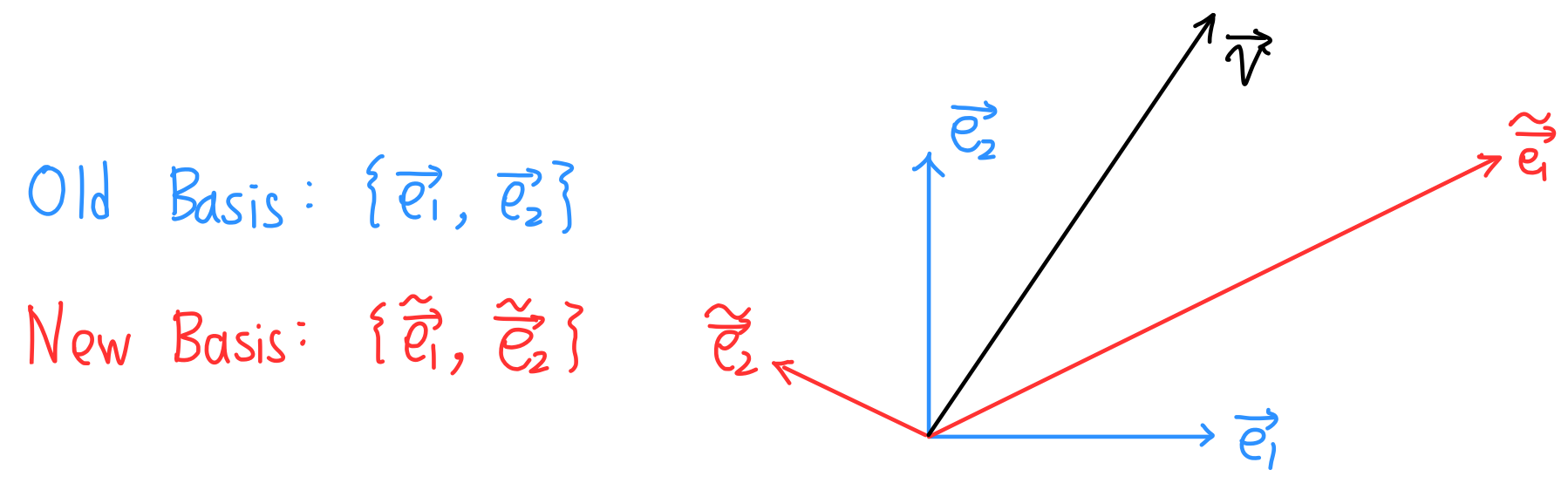
임의의 벡터 $\overrightarrow{v}$ 를 서로 다른 basis로 표현하면 다음과 같이 쓸 수 있습니다.
$$\overrightarrow{v} = v^j \overrightarrow{e_j} = \widetilde{v}^i \widetilde{\overrightarrow{e_i}}$$
Einstein summation convention을 이용하여 표현한 것이기 때문에 $i$ 와 $j$ 대신 어떤 기호를 사용해도 상관없습니다.
Basis vector transformation은 covariant transformation 이기에 다음과 같이 쓸 수 있습니다.
$$\widetilde{\overrightarrow{e_j}} = F_j^i \overrightarrow{e_i}$$
$$\overrightarrow{e_j} = B_j^i \widetilde{\overrightarrow{e_i}}$$
따라서 다음과 같이 식을 전개할 수 있습니다.
$$\overrightarrow{v} = v^j \overrightarrow{e_j} = v^j (B_j^i \widetilde{\overrightarrow{e_i}}) = (v^j B_j^i) \widetilde{\overrightarrow{e_i}}=\widetilde{v}^i \widetilde{\overrightarrow{e_i}}$$
따라서 다음의 사실을 알 수 있습니다.
$$\widetilde{v}^i = B_j^i v^j$$
비슷한 과정을 통해, 다음의 수식도 유도할 수 있습니다.
$$v^i = F_j^i \widetilde{v}^j$$
이렇게 기존의 vector components transformation이 contravariant transformation임을 간단하게 보였습니다.
Derivative Transformation
우선 derivative 수식을 갖고 오겠습니다.
$$\dfrac{d \overrightarrow{R}}{d \lambda} = \dfrac{dc^j}{d\lambda}\dfrac{\partial \overrightarrow{R}}{\partial c^j} = \dfrac{dp^i}{d\lambda}\dfrac{\partial \overrightarrow{R}}{\partial p^i}$$
지난 포스트 [tensor calculus] 1. The Jacobian & Einstein summation convention 에서 Chain rule을 이용하여 basis vector 사이에 다음과 같은 관계가 있다는 것을 보였습니다.
$$\dfrac{\partial \overrightarrow{R}}{\partial p^j} = \dfrac{\partial c^i}{\partial p^j}\dfrac{\partial \overrightarrow{R}}{\partial c^i}$$
$$\dfrac{\partial \overrightarrow{R}}{\partial c^j} = \dfrac{\partial p^i}{\partial c^j}\dfrac{\partial \overrightarrow{R}}{\partial p^i}$$
이를 derivative 수식에 넣어 전개하면 다음과 같이 됩니다.
$$\dfrac{d \overrightarrow{R}}{d \lambda} = \dfrac{dc^j}{d\lambda}\dfrac{\partial \overrightarrow{R}}{\partial c^j}= \dfrac{dc^j}{d\lambda}\left(\dfrac{\partial p^i}{\partial c^j}\dfrac{\partial \overrightarrow{R}}{\partial p^i}\right)= \left(\dfrac{dc^j}{d\lambda}\dfrac{\partial p^i}{\partial c^j}\right)\dfrac{\partial \overrightarrow{R}}{\partial p^i}=\dfrac{dp^i}{d\lambda}\dfrac{\partial \overrightarrow{R}}{\partial p^i}$$
따라서 다음의 사실을 알 수 있습니다.
$$\dfrac{dp^i}{d\lambda}=\dfrac{\partial p^i}{\partial c^j}\dfrac{dc^j}{d\lambda}$$
비슷한 과정을 통해, 다음의 수식도 유도할 수 있습니다.
$$\dfrac{dc^i}{d\lambda}=\dfrac{\partial c^i}{\partial p^j}\dfrac{dp^j}{d\lambda}$$
수식 정리
지금까지 나온 수식을 정리하면 다음과 같습니다.
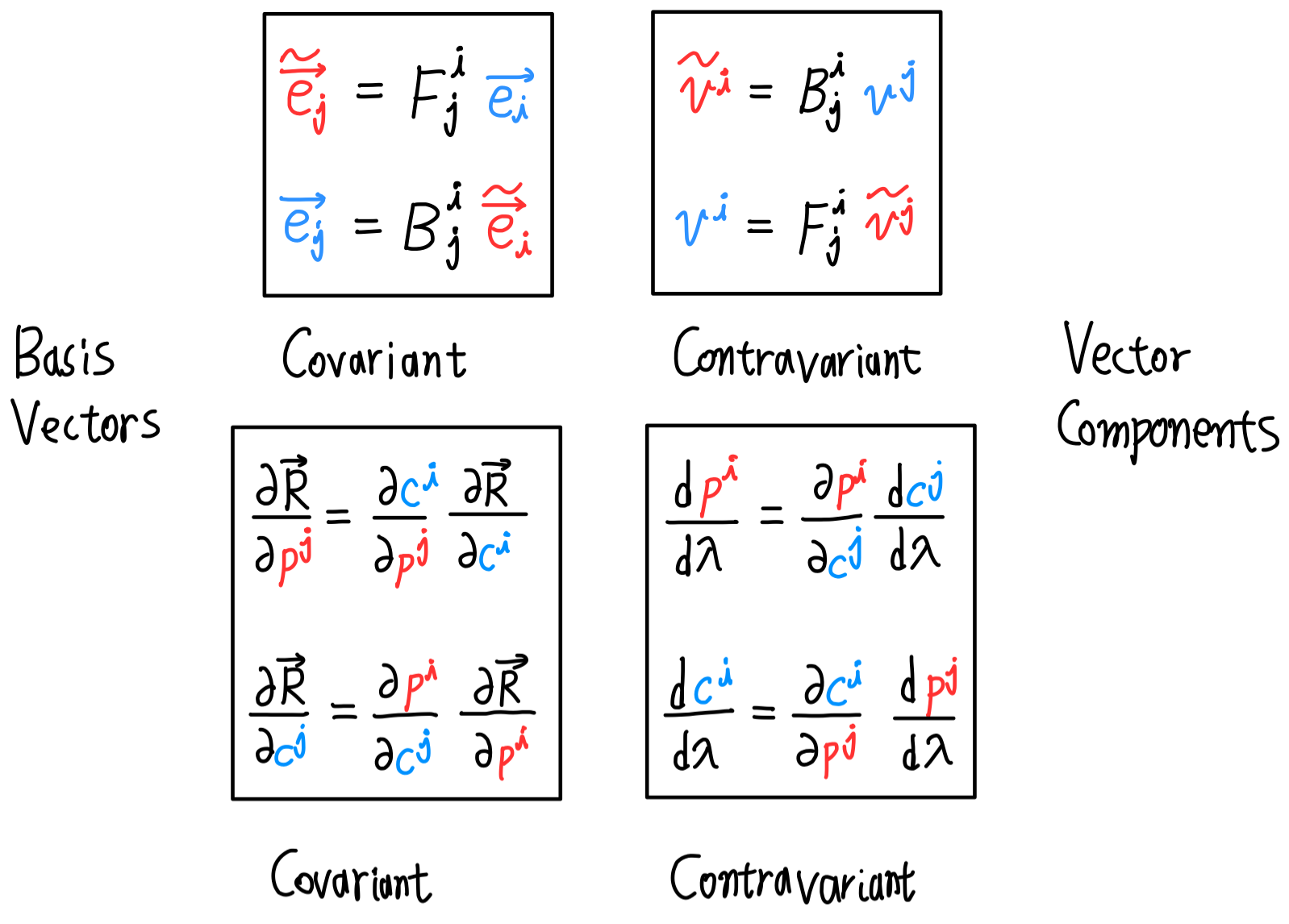
Jacobian matrix와 Inverse Jacobian matrix를 먼저 구해봅시다.
$$\mathbf{J}=\begin{bmatrix} \dfrac{\partial c^1}{\partial p^1} & \dfrac{\partial c^1}{\partial p^2} \\ \dfrac{\partial c^2}{\partial p^1} & \dfrac{\partial c^2}{\partial p^2} \end{bmatrix} = \begin{bmatrix} \cos \theta & -r \sin \theta \\ \sin \theta & r \cos \theta \end{bmatrix} = \begin{bmatrix} \cos \theta & -2 \sin \theta \\ \sin \theta & 2 \cos \theta \end{bmatrix}$$
Jacobian & Vector components transformation
[tensor calculus] 0. Introduction에서 다루었던 것을 떠올려봅시다.
해당 포스트에서 아래와 같은 수식이 나왔었습니다.
$$ {\begin{bmatrix} 1 \\ 2 \\ \end{bmatrix}}_{\widetilde{\overrightarrow{e_{i}}}} = B {\begin{bmatrix} 1 \\ 1.5 \\ \end{bmatrix}}_{\overrightarrow{e_{i}}}$$
$$B = \begin{bmatrix} \frac{1}{4} & \frac{1}{2} \\ -1 & 2 \\ \end{bmatrix}$$
저희가 이번 포스트에서 다룬 vector components 변환도 위와 같이 행렬로 나타내고 싶습니다.
즉, 아래와 같은 수식으로 vector components간의 관계를 나타내고 싶은 것입니다.(아래 수식의 아래 첨자가 아까 다룬 내용과는 약간 달라졌습니다. $\overrightarrow{R}$이 분자에서 사라졌습니다. 이렇게 적어도 괜찮으며, 그 이유는 아래의 "Extrinsic vs Intrinsic + New notation" 파트에서 다루겠습니다.)
$${\begin{bmatrix} 0 \\ 1 \\ \end{bmatrix}}_{\frac{\partial}{\partial c^i}} = B {\begin{bmatrix} -2 \sin(\lambda) \\ 2\cos(\lambda) \\ \end{bmatrix}}_{\frac{\partial}{\partial p^i}}$$
이 때 $B$ 는 과연 무엇일까요?
바로 $B = \mathfb{J}^{-1}$ 입니다.
수식적인 증명은 간단합니다.
단순히 위의 수식정리 된 그림 중 오른쪽 아래 네모 박스의 첫번째 수식을 행렬로 표현하면 그렇게 된다는 것을 쉽게 알 수 있습니다.
증명은 생략하고, 직접 실질적인 값을 넣어보며 변환이 잘 되는지 보겠습니다.
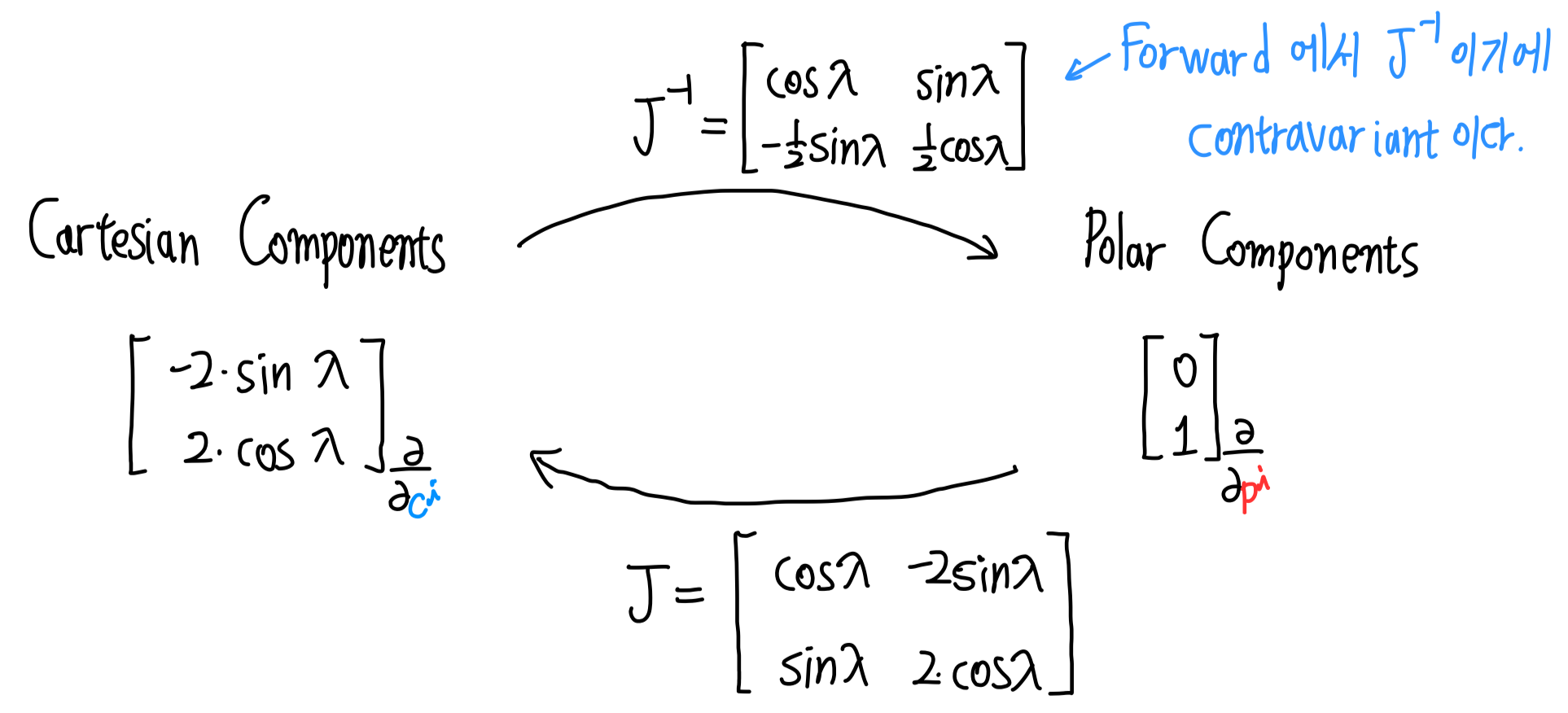
다시 예시 그림을 갖고 오겠습니다.

Jacobian matrix와 Inverse Jacobian matrix를 먼저 구해봅시다.
$c^1=x(\lambda) $, $c^2=y(\lambda) $, $p^1=r(\lambda)$, $p^2=\theta(\lambda)$ 는 이미 이전에 구했기 때문에 구하는 과정을 생략하겠습니다.
$$\mathbf{J}=\begin{bmatrix} \dfrac{\partial c^1}{\partial p^1} & \dfrac{\partial c^1}{\partial p^2} \\ \dfrac{\partial c^2}{\partial p^1} & \dfrac{\partial c^2}{\partial p^2} \end{bmatrix} = \begin{bmatrix} \cos \lambda & -r \sin \lambda \\ \sin \lambda & r \cos \lambda \end{bmatrix} = \begin{bmatrix} \cos \lambda & -2 \sin \lambda \\ \sin \lambda & 2 \cos \lambda \end{bmatrix}$$
$$\mathbf{J}^{-1}=\begin{bmatrix} \dfrac{\partial p^1}{\partial c^1} & \dfrac{\partial p^1}{\partial c^2} \\ \dfrac{\partial p^2}{\partial c^1} & \dfrac{\partial p^2}{\partial c^2} \end{bmatrix} = \begin{bmatrix} \dfrac{x}{r} & \dfrac{y}{r} \\ -\dfrac{x}{r^2} & \dfrac{y}{r^2} \end{bmatrix} = \begin{bmatrix} \cos \lambda & \sin \lambda \\ -\dfrac{1}{2}\sin \lambda & \dfrac{1}{2} \cos \lambda \end{bmatrix}$$
이제 Vector components transformation이 잘 되는지 확인해보겠습니다!
Forward Transformation은 다음과 같이 계산됩니다.
$$\begin{align*} \mathbf{J}^{-1} \begin{bmatrix} -2\sin\lambda \\ 2\cos\lambda \end{bmatrix}_{\frac{\partial}{\partial c^i}} &= \begin{bmatrix} \cos \lambda & \sin \lambda \\ -\dfrac{1}{2}\sin \lambda & \dfrac{1}{2} \cos \lambda \end{bmatrix} \begin{bmatrix} -2\sin\lambda \\ 2\cos\lambda \end{bmatrix}_{\frac{\partial}{\partial c^i}} \\ &= \begin{bmatrix} -2\sin\lambda\cos\lambda + 2\sin\lambda\cos\lambda \\ \sin^2\lambda + \cos^2\lambda \end{bmatrix}_{\frac{\partial}{\partial p^i}} \\ &= \begin{bmatrix} 0 \\ 1 \end{bmatrix}_{\frac{\partial}{\partial p^i}}\end{align*}$$
Backward Transformation은 다음과 같이 계산됩니다.
$$\begin{align*} \mathbf{J} \begin{bmatrix} 0 \\ 1 \end{bmatrix}_{\frac{\partial}{\partial p^i}} &= \begin{bmatrix} \cos \lambda & -2 \sin \lambda \\ \sin \lambda & 2 \cos \lambda \end{bmatrix} \begin{bmatrix} 0 \\ 1 \end{bmatrix}_{\frac{\partial}{\partial p^i}} \\ &= \begin{bmatrix} -2\sin\lambda \\ 2\cos\lambda \end{bmatrix}_{\frac{\partial}{\partial c^i}}\end{align*}$$
잘 됩니다! 그림으로 정리하면 다음과 같이 됩니다.
Extrinsic vs Intrinsic + New notation
지난 포스트 [tensor calculus] 1. The Jacobian & Einstein summation convention 에서 저희는 다음과 같은 수식을 보았었습니다.
$$\begin{align*} \overrightarrow{e_x}= \dfrac{\partial \overrightarrow{R}}{\partial x} \qquad \overrightarrow{e_y} =\dfrac{\partial \overrightarrow{R}}{\partial y} \\ \widetilde{\overrightarrow{e_r}} = \dfrac{\partial \overrightarrow{R}}{\partial r} \qquad \widetilde{\overrightarrow{e_\theta}} = \dfrac{\partial \overrightarrow{R}}{\partial \theta} \end{align*}$$
하지만 이러한 공식은 사용하기 어려운 경우가 있습니다.
Curved 2D surface인 지구 표면에서의 Extrinsic Geometry와 Intrinsic Geometry를 예시로 들며 설명하겠습니다.
Extrinsic Geometry
Extrinsic Geomerty은 객체가 임베딩된 더 큰 공간을 고려하여 그 객체의 기하학적 속성을 연구합니다. 이러한 접근 방식에서는 대상이 놓인 주변 공간의 관계를 통해 대상의 형태와 구조를 이해하려고 합니다. 예를 들어, 3차원 공간에 임베딩된 2차원 곡면의 곡률 같은 속성을 3차원 세상에 사는 관찰자 관점에서 탐구할 수 있습니다.
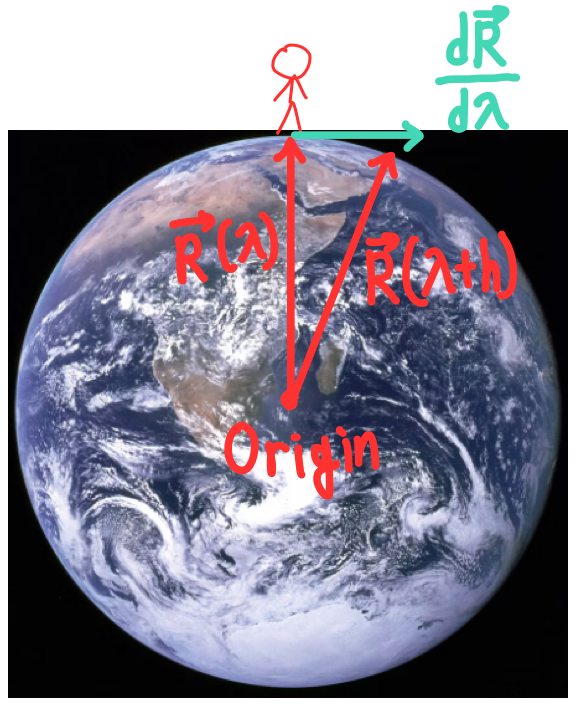
지구의 중심을 origin으로 잡으면, 지구 표면에 있는 사람의 위치를 위치 벡터를 $\overrightarrow{R}$ 로 잡을 수 있습니다.
$\overrightarrow{R}$ 을 좌표를 사용하여 나타내려면 3개의 항이 필요할 것 입니다.
지구 표면위의 사람이 $\lambda$에 따라 위치가 바뀐다고(걸어다닌다고) 합시다.
그러면 $\dfrac{d \overrightarrow{R}}{d\lambda} = \lim_{h \to 0}\dfrac{\overrightarrow{R}(\lambda + h)-\overrightarrow{R}(\lambda)}{h}$ 을 통해 지구 표면 위의 사람의 속도를 구할 수 있습니다.
위의 그림을 보면 다음과 같은 두 가지 특징을 찾을 수 있습니다.
- Origin이 지구 표면 2D space에 있지 않습니다.
- 속도 벡터 $\dfrac{d \overrightarrow{R}}{d\lambda}$ 가 표면 바깥에 존재합니다.
Intrinsic Geometry
Intrinsic Geometry는 객체의 내부에서 정의되고 측정될 수 있는 기하학적 속성에 중점을 둡니다. 이는 객체가 임베딩된 외부 공간의 구조에 의존하지 않고, 대신 객체 자체의 관점에서 공간의 구조를 이해하려고 합니다. 예를 들어, 곡면 위를 이동하는 생물체가 곡면의 곡률을 "느끼지" 못하는 것처럼, 내재적 기하학은 공간이나 형태를 그 안에서 경험하는 방식에 초점을 맞춥니다. 이 관점에서, 거리, 각도, 곡률 등은 객체의 내부 구조만을 사용하여 정의됩니다.
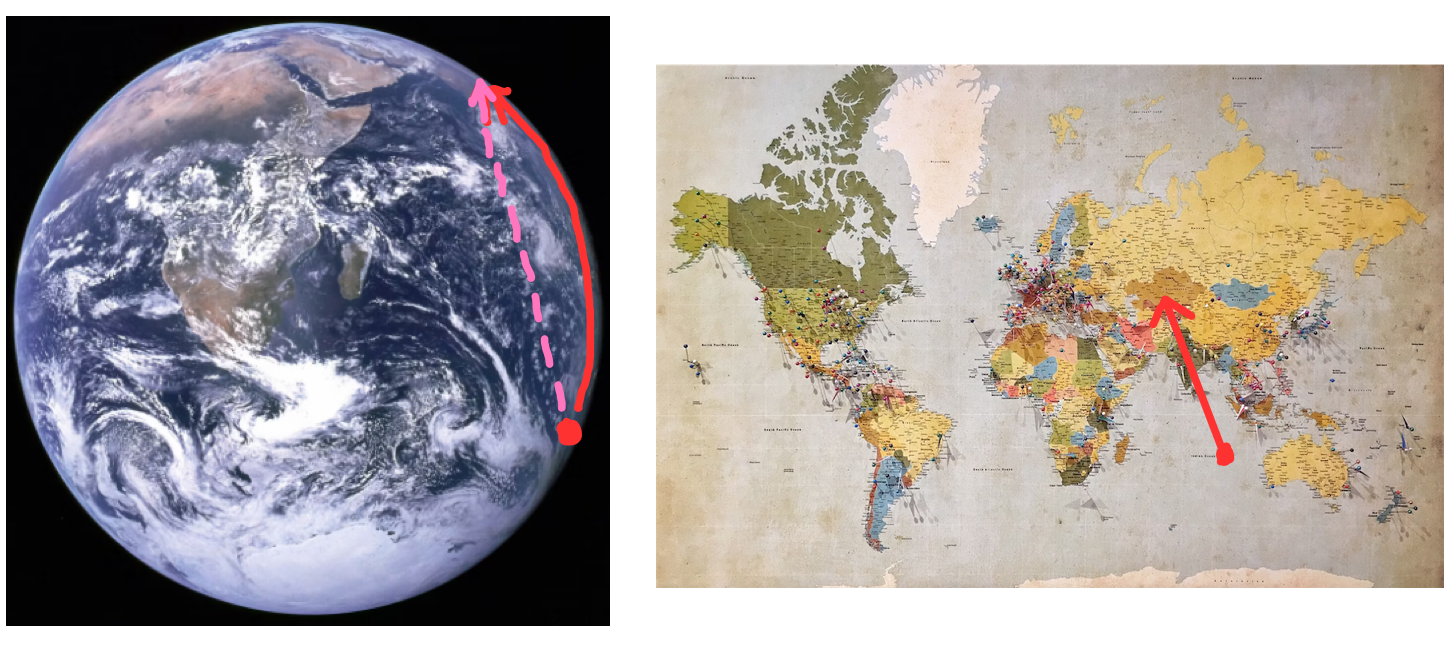
위 그림의 오른쪽 세계 지도를 보시기 바랍니다. 이는 지구 표면을 평면으로 펼친 그림입니다.
오른쪽 세계 지도에서의 빨간색 화살표를 따라 사람이 걸어간다고 합시다.
이를 3차원에 임베딩된 지구 표면(왼쪽 그림)에서 경로를 그려보면 분홍색 선처럼 뚫고 들어가는 것이 아닌, 빨간색 선처럼 표면을 따라가는 경로가 그려지게 될 것입니다.
Intrinsic geometry는 그 객체에서 기어다니는 벌레의 입장에서 생각을 하는 것이라고 생각하면 됩니다.
그들은 자신이 사는 세상보다 더 큰 차원 바깥으로 나가는 속도 벡터를 상상하지 못하고, 더 큰 차원에 존재하는 origin을 고려할 수 없습니다.
즉, Intrinsic geometry는 그 객체보다 더 큰 공간을 고려하지 못하고, 그렇기에 더 큰 공간에서의 origin을 고려할 수 없습니다.
이러한 Intrinsic geometry는 우리가 사는 세상을 이해하기 위해 필요한 분야입니다. 우리가 사는 우주 시공간은 4D curved 공간이라고 알려져 있고, 그 공간에서만 사는 우리는 이보다 더 큰 차원에 존재하는 Origin을 상상할 수 없기 때문입니다.
그래서 Intrinsic geometry에서는 $\overrightarrow{R}$ 을 도입하지 않고, 방향을 설명할 때는 derivative operator만을 사용하여 나타냅니다. 아래와 같이 말이죠.
$$\begin{align*} \overrightarrow{e_x}= \dfrac{\partial}{\partial x} \qquad \overrightarrow{e_y} =\dfrac{\partial}{\partial y} \\ \widetilde{\overrightarrow{e_r}} = \dfrac{\partial}{\partial r} \qquad \widetilde{\overrightarrow{e_\theta}} = \dfrac{\partial}{\partial \theta} \end{align*}$$
앞으로는 위와 같은 표기를 많이 사용할 것입니다!
이번 포스트는 여기까지입니다!
'취미 > 수학' 카테고리의 다른 글
| [tensor calculus] 1. The Jacobian & Einstein summation convention (0) | 2024.03.06 |
|---|---|
| [tensor calculus] 0. Intorduction (0) | 2024.02.12 |

